• 内核数据结构
  • 链表
    • 单向和双向链表
    • 循环链表
    • 遍历链表
    • linux内核的实现
      • 链表结构
      • 定义一个链表
      • 链表头
    • 操作链表
      • 在链表中添加一个元素
      • 从链表中删除一个元素
      • 移动或者拼接链表
    • 遍历链表
      • 基础的方法
      • 可用的方法
      • 反向遍历
      • 遍历的时候删除
      • 其他的链表方法
  • 队列
    • kfifo
    • 创建队列
    • 入队列
    • 出队列
    • 获取队列的大小
    • 重置和销毁队列
    • 队列的使用例子
  • Maps
  • 二叉树
    • 二叉搜索树
    • 自平衡的二叉搜索树
      • 红黑树
      • rbtrees
  • 什么时候采用什么数据结构
  • 算法复杂度

内核数据结构

这一章介绍一些在内核代码中会用到的内建数据结构。和其他大型软件项目一样，内核提供了这些通用的数据结构鼓励代码重用。内核开发者在任何时候都应该尽量使用这些数据结构，而不是造轮子（使用自己的解决方案）。在下面的章节中，会覆盖如下的数据结构:

• Linked lists
• Queues
• Maps
• Binary trees

在章节的结尾，我们会讨论算法和数据结构在支撑大型输入的时候的算法复杂度。

链表

Linked Lists（下面称为链表）是内核中最简单最通用的数据结构。链表用于存储数据，内部可存储的节点数是可变的，存储的元素称为nodes。不像静态的数组，链表可以动态的创建和插入节点。即使在编译时刻不知道节点的数目，链表仍然可以存储和管理数据。因为链表内部的元素是在不同时刻创建的，所以内部的元素不需要占用连续的内存空间。因此，链表内部的元素需要链接在一起。链表内的每一个元素包含一个指向下一个元素的指针。当插入或者删除数据的时候，指向下一个元素的指针需要做简单的调整。

单向和双向链表

最简单的链表的实现和下面的代码类似:

/* an element in a linked list */
struct list_element {
    void *data; /* the payload */
    struct list_element *next; /* pointer to the next element */
};

下面的图可以更形象的展示链表是如何实现的，

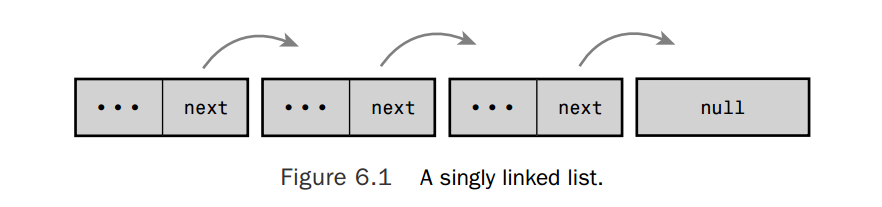
在某些链表中，元素还包含指向前一个元素的指针。这些链表被称为双向链表，通过链表中一个元素可以向前查找到之前的元素或者向后查找到之后的元素。如上面的那附图所示，这种不包含前向指针的链表被称为单向链表。

双向链表的实现和下面的代码类似，

/* an element in a linked list */
struct list_element {
void *data; /* the payload */
    struct list_element *next; /* pointer to the next element */
    struct list_element *prev; /* pointer to the previous element */
};

下面的图可以更形象的展示双向链表是如何实现的，

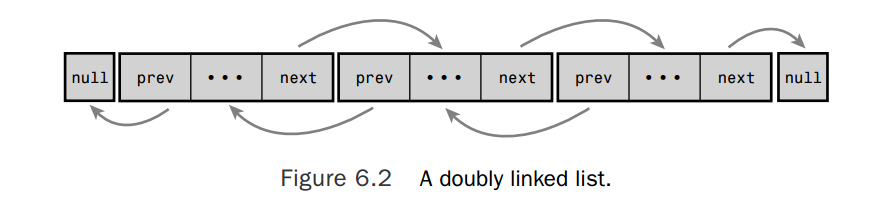
循环链表

通常情况下，链表中的最后一个元素的next指针没有指向下一个元素，所以会被设置为一个特殊的值，比如NULL。在某些特殊的链表中，最后一个元素的next指针没有设置为特殊的值。相反，它指向了链表中的第一个元素。在这种情况下，链表被称为循环链表，因为链表是一个环。循环链表可以是单向，也可以是双向的链表。如果是双向的循环链表，那么第一个元素的previous指针指向了最后一个元素。下面的两个图展示了单向和双向的循环链表，

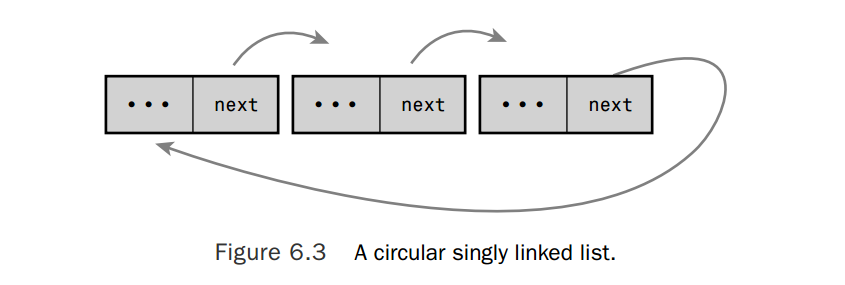
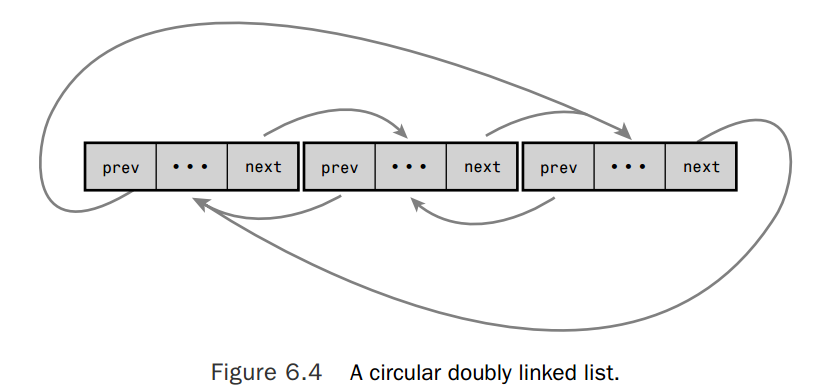
Linux内核的链表实现是唯一的，本质上是一个双向链表。使用这种链表可以提供最大的便利

遍历链表

链表的遍历是线性的。访问一个元素后，跟着next指针访问下一个数据，循环往复，遍历整个链表。这是遍历链表最简单的方法，也是遍历链表最合适的方法。链表不适用于那些需要随机访问的重要操作。当遍历、动态的插入和删除是必要的操作的时候，你应该使用链表。

在链表的实现中，链表中的第一个元素通常使用一个特殊的指针表示–这个指针被称作head，这样可以方便的访问链表的开头。在非循环链表中，最后一个元素的next指针设置为NULL。在循环链表中，最后一个元素的next指针指向了链表的第一个元素（头元素）。遍历链表就是从第一个元素开始逐个访问直到最后一个元素。在双向链表中，遍历操作可以是反向的，也就是说从最后一个元素开始逐个访问直到第一个元素。当然，给定一个元素，你既可以向前也可以向后遍历。

linux内核的实现

和大多数链表的实现相比（包括上面提到的），Linux内核中链表的实现是独特的。回顾之前的讨论，链表通过一个next指针指向下一个元素，然后将整个链表串联起来。举个例子，假如我们有一个fox结构用来描述犬科中的一员:

struct fox {
    unsigned long tail_length; /* length in centimeters of tail */
    unsigned long weight; /* weight in kilograms */
    bool is_fantastic; /* is this fox fantastic? */
};

如果想要将该结构存储在链表中，常规的做法是在结构中加入链表指针next和prev。比如下面这样，

struct fox {
    unsigned long tail_length; /* length in centimeters of tail */
    unsigned long weight; /* weight in kilograms */
    bool is_fantastic; /* is this fox fantastic? */
    struct fox *next; /* next fox in linked list */
    struct fox *prev; /* previous fox in linked list */
};

linux的实现方式是不同的。它不是将对应的结构转化为链表，而是在结构中嵌入一个链表节点。

链表结构

在过去，内核中有多个版本的链表实现，因此需要一个强大的链表实现来移除重复的代码。在内核的2.1版本中，内核官方的链表实现首次被引入。现在内核中使用链表的地方，都是使用的官方实现，而不是自己造轮子。

链表的代码在头文件<linux/list.h>中，并且数据结构也很简单:

struct list_head {
    struct list_head *next
    struct list_head *prev;
};

next指针指向下一个元素，prev指针指向前一个元素。从表面来看，这个结构没有太大的用处。下面是list_head的具体用法，

struct fox {
    unsigned long tail_length; /* length in centimeters of tail */
    unsigned long weight; /* weight in kilograms */
    bool is_fantastic; /* is this fox fantastic? */
    struct list_head list; /* list of all fox structures */
};

这样改动后，list.next指向了下一个元素，list.prev指向了前一个元素。这样实现相比于之前更加简洁，并且将业务和链表逻辑解耦，显得更加优雅。内核提供了一系列的方法来操作链表。比如，list_add()方法用于在一个已经存在的链表中添加一个新的节点。这些方法是通用的: 它们只接受list_head作为输入。使用宏定义container_of()，我们可以轻松的获取到包含了链表结构的父结构。因为在C语言中，结构中的一个属性在结构中的偏移量在编译时期是确定的。

#define container_of(ptr, type, member) ({ \
        const typeof( ((type *)0)->member ) *__mptr = (ptr); \
        (type *)( (char *)__mptr - offsetof(type,member) );})

使用container_of()，我们可以定义一个简单的方法来返回包含任意list_head的父结构:

#define list_entry(ptr, type, member) \
        container_of(ptr, type, member)

通过list_entry()，内核提供方法来创建、操作链表，而无需直到list_head所在父结构的任何信息。

定义一个链表

如上面所示，一个单一的list_head是没有意义的。它必须嵌入到对应的结构中区:

struct fox {
    unsigned long tail_length; /* length in centimeters of tail */
    unsigned long weight; /* weight in kilograms */
    bool is_fantastic; /* is this fox fantastic? */
    struct list_head list; /* list of all fox structures */
};

链表在使用之前必须初始化好。因为大多数的元素都是动态创建的，初始化链表的通常方式是在运行时创建:

struct fox *red_fox;
red_fox = kmalloc(sizeof(*red_fox), GFP_KERNEL);
red_fox->tail_length = 40;
red_fox->weight = 6;
red_fox->is_fantastic = false;
INIT_LIST_HEAD(&red_fox->list);

如果需要在编译时刻创建，你可以通过如下简单的方式:

struct fox red_fox = {
.tail_length = 40,
.weight = 6,
.list = LIST_HEAD_INIT(red_fox.list),
};

链表头

前面的小节展示了将一个已经存在的结构转化为链表结构是多么的容易。通过最简单的代码改动，我们就可以通过内核提供的链表方法来操作已有的结构。但是在我们使用这些方法之前，我们需要获取链表的头指针。

内核链表一个好的方面是fox节点都是等价的。每一个节点都包含list_head，我们可以从任意一个节点访问到下一个节点，直到我们遍历所有节点。这种方式很优雅，但是你通常需要一个特殊的指针来代表你的链表。有趣的是，这个特殊的节点仅仅是一个普通的list_head:

static LIST_HEAD(fox_list);

上面的宏定义并且初始化了一个list_head，对应的名字是fox_list。绝大多数的链表相关的方法接收一个或者两个参数:链表头或者链表头加上实际的一个节点。下面，让我们来看看这些方法。

操作链表

内核提供了一系列的方法来操作链表。他们接收一个或者多个list_head结构作为参数。这些方法都是内联方法，采用c实现，定义在<linux/list.h>中。

有趣的是，这些方法的时间复杂度是O(1).这意味着执行这些方法的时间是常量，无论列表的大小是多大。例如，无论列表的大小是3或者3000，天假一个元素或者移除一个元素的时间都是相同的。这对你来说也许不足为奇，但是还是有必要知道的。

在链表中添加一个元素

在链表中添加一个元素:

list_add(struct list_head *new, struct list_head *head)

上面的方法在head节点后面插入新的节点。因为链表是循环的，所以没有首节点和尾节点的概念，你可以传递任意元素当做head节点。如果你将尾节点传递到该方法，那么该方法可以用来实现栈。

回到之前的例子fox，假设我们有一个新的fox结构需要添加到```fox_list``中。我们可以这么做:

list_add(&f->list, &fox_list);

可以通过下面的方法添加节点到链表的尾部:

list_add_tail(struct list_head *new, struct list_head *head)

这个方法将节点添加到head节点的前面。因为链表是循环的，所以你可以传递任意的节点当做head节点。如果你传递第一个节点当做head节点，那么可以用来实现队列。

从链表中删除一个元素

除了添加元素，从链表中删除另一个比较重要的操作。使用list_del()可以从链表中删除一个元素:

list_del(struct list_head *entry)

这个方法从链表中移除一个元素。需要注意的是，它不释放链表元素或者链表元素所在的父结构所占用的内存；这个方法仅仅是将元素从链表中移除。在调用这个方法后，你需要手动销毁（释放内存）list_head和其所在的结构。

举个例子，删除我们之前添加到fox_list中的元素:

list_del(&f->list);

需要注意的这个方法不是将for_list作为参数。它仅仅接收一个特定的节点，并且修改该节点之前的节点和之后节点的指针。实现如下所示:

static inline void __list_del(struct list_head *prev, struct list_head *next)
{
    next->prev = prev;
    prev->next = next;
}
static inline void list_del(struct list_head *entry)
{
    __list_del(entry->prev, entry->next);
}

内核提供了一个方法在删除一个节点的同时重新初始化该节点:

list_del_init(struct list_head *entry)

这个方法的作用和之前的list_del()类似，除了它会重新初始化list_head，当然这么做是有假设条件的:你不想该节点出现在列表中，但是又希望重用该数据结构。

移动或者拼接链表

把一个节点从一个链表移动到另一个链表:

list_move(struct list_head *list, struct list_head *head)

该方法将一个节点从给定的链表中移除，并且插入到另一个链表的head节点之后。

把一个节点从一个节点移动到另一个链表的尾部:

list_move_tail(struct list_head *list, struct list_head *head)

该方法和list_move()类似，但是是把元素插入到head之前。

检查一个链表是否为空:

list_empty(struct list_head *head)

如果链表不为空，该函数返回非0；否则返回0。

把两个链表连接起来:

list_splice(struct list_head *list, struct list_head *head)

该方法将list指向的链表插入到另一个链表的head元素之后。

将两个链表链接起来，并且将老的链表重新初始化:

list_splice_init(struct list_head *list, struct list_head *head)

该方法和list_splice()类似，除了list指向的链表需要重新初始化外。

如果你已经有了next和prev指针，你可以通过直接调用内部的链表函数来节省一些执行时间（cycles）。上面提到的几个函数实际上只是了查找next和prev指针然后调用内部函数意外。所有的内部函数都有与其同名的封装函数，内部函数都是以双下划线开头。比如，如果你不调用list_del(list)，那么可以直接调用 __list_del(prev, next)。只有在next指针和prev指针都已经准备好的时候，才可以直接调用内部函数。

遍历链表

现在你已经直到如何在内核中声明，初始化和操作一个链表了。能做到这样已经很好了，但是如果你无法访问你的数据这一切就显得无意义了。链表只是存储你的重要数据的载体；你需要方法来访问实际的数据；内核提供了一系列方法遍历链表，同时访问包含链表元素的数据结构。

你需要注意的是，不像其他的操作方法，遍历链表的复杂度是O(n)的。

基础的方法

遍历链表的最基础方法是宏list_for_each()。这个宏有两个参数，都是list_head类型。第一个参数是指向当前元素的指针，它是你必须提供的一个临时变量。第二个参数作为你想遍历的链表的head节点。在每次循环，第一个参数指向下一个元素，直到所有的元素都被访问过了。使用的方式如下所示:

struct list_head *p;
list_for_each(p, fox_list) {
    /* p points to an entry in the list */
}

好了，到目前为止仍然是没有太大意义的！只有一个指向当前链表结构的指针是不够的；我们需要的是包含该指针结构的父结构的指针。已之前的fox为例，我们需要的是指向fox的指针，而不是指向fox中的list的指针。我们可以使用之前讨论过的宏list_entry()来获取包含list_head的父结构。例如:

struct list_head *p;
struct fox *f;
list_for_each(p, &fox_list) {
    /* f points to the structure in which the list is embedded */
    f = list_entry(p, struct fox, list);
}

可用的方法

上面提到的遍历的方法不够直观，并且代码不够优雅，尽管它能够展示如何通过list_head获取数据的。因此，大多数内核代码使用宏list_for_each_entry()来遍历链表。list_for_each_entry()通过list_entry()来获取数据，使得循环相对简单:

list_for_each_entry(pos, head, member)

pos 是指向包含list_head的对象。可以将其理解为list_entry() 的返回值。head是指向head节点的指针–在之前的例子中该值为fox_list。member是list_head 在pos所指向的结构中的名称–在之前的例子中member为list。这听起来挺让人困惑，但是使用起来却很方便。下面的代码展示了如何使用list_for_each_entry()来替代之前的list_for_each:

struct fox *f;
list_for_each_entry(f, &fox_list, list) {
    /* on each iteration, ‘f’ points to the next fox structure ... */
}

下面我们看一个真实的例子inotify，这个例子来自内核文件系统的通知系统:

static struct inotify_watch *inode_find_handle(struct inode *inode,
struct inotify_handle *ih)
{
    struct inotify_watch *watch;
    list_for_each_entry(watch, &inode->inotify_watches, i_list) {
        if (watch->ih == ih)
            return watch;
    }
    return NULL;
}

这个函数遍历inode->inotify_watches中的所有元素。链表中的元素是struct inotify_watch，list_head在对应的父结构的名称是i_list。在每次遍历的时候，watch指向了当前的节点。

反向遍历

宏list_for_each_entry_reverse()和list_for_each_entry()类似，除了它是反向遍历链表。它不是使用next指针向后遍历，而是使用prev指针向前遍历。使用的方法和list_for_each_entry()类似:

list_for_each_entry_reverse(pos, head, member)

只有少数的几个理由让你选择反向遍历链表。一个理由是性能:你可以确定你所搜索的节点位于搜索起始节点的后面（注释1），这时候反向遍历可以更快速的找到对应的节点。第二个理由是顺序十分必要。例如如果你把链表当做栈来用，你需要从尾节点开始反向遍历，已达到后进先出的顺序。如果你没有明显的原因，那么还是使用list_for_each_entry()来遍历链表。

注释1: A -> B -> C。将链表理解为一个赛道，链表上的每个节点是赛车。这时候B要追赶C，同时B已经超越了A，所以可以说A在B的后面。

遍历的时候删除

当你需要在遍历的时候删除相应的节点的时候，常规的遍历方法是不合适的。常规的遍历方法是基于你在遍历的时候各个节点是不会改变的事实，因此如果在循环的过程中节点被删除了，无法通过当前节点的next指针获取后面的遍历内容。这是循环的一个通常模式，开发者可以通过在移除之前将next存储在一个临时变量来解决上面得问题。linux的内核提供了一个方法来解决上述问题:

list_for_each_entry_safe(pos, next, head, member)

你可以按照使用list_for_each_entry()的方式来使用上面的方法，除了你必须提供一个next指针之外，next指针的类型和pos一样。next指针用于存储链表中的下一个元素，使得删除操作是安全的。让我们来看一下下面的例子，同样来自inotify:

void inotify_inode_is_dead(struct inode *inode)
{
    struct inotify_watch *watch, *next;
    mutex_lock(&inode->inotify_mutex);
    list_for_each_entry_safe(watch, next, &inode->inotify_watches, i_list) {
        struct inotify_handle *ih = watch->ih;
        mutex_lock(&ih->mutex);
        inotify_remove_watch_locked(ih, watch); /* deletes watch */
        mutex_unlock(&ih->mutex);
    }
    mutex_unlock(&inode->inotify_mutex);
}

上面的函数遍历链表，并且移除所有的inotify_watch节点。如果使用常规的list_for_each_entry()，上面的代码会出现bug，当通过watch获取下一个节点的时候，watch已经被销毁了。

如果你需要反向遍历链表，并且删除元素，那么你应该使用list_for_each_entry_safe_reverse():

list_for_each_entry_safe_reverse(pos, n, head, member)

上面方法的使用和list_for_each_entry_safe()一样。

你可能还需要锁!
如果你在循环体内只删除对应的节点，那么list_for_each_entry()可以保证安全。如果存在并发的删除，或者其他的并发操作，那么你需要对相应的链表加锁。

其他的链表方法

linux内核还提供了其他很多的链表相关的函数，你几乎有所有的方式来访问和操作链表。所有的这些函数定义在头文件<linux/list.h>中。

队列

几乎所有的操作系统内核都有一个通用的编程模式生产者和消费者模式。在这种模式中，生产者生成数据–异常消息或者待处理的网络包，同时消费者读取数据，然后处理数据。实现这种模式的最简单的方法是使用队列。生产者将数据推送到队列中，然后消费者从队列拉取数据。生产者按照消息进队列的顺序来获取数据。也就是说，第一个进入队列的数据，也会是第一个出队列的。所以，队列被称作FIFOs，FIFOs是first-in, first-out的简称。下面的图是一个标准队列的例子。

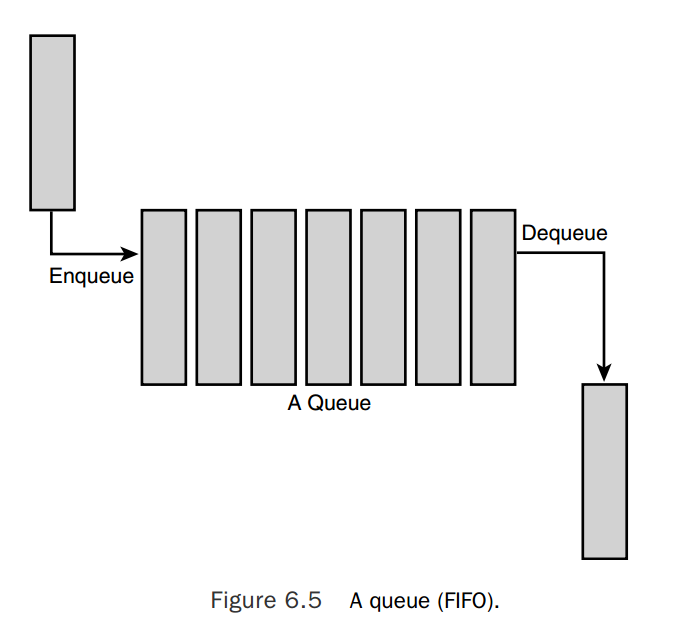
linux内核中通用的队列实现叫做kfifo，kfifo的实现位于kernel/kfifo.c中，并且生命在<linux/kfifo.h>中。

kfifo

linux的kfifo和大多的队列一样，提供了两个主要的操作:入队列和出队列。kfifo中维护了两个偏移量:in offset和out offset。in offset在队列中表明下一个进入到队列的数据所处的位置。out offset表示下一个出队列的数据所在的位置。out offset通常情况下是小于等于in offset的。前者大于后者是没有意义的，因为你可能会将原本还进入到队列的数据出队列。

入队列操作将数据拷贝到队列中，数据位于in offset。当拷贝完成，in offset会根据拷贝的数据的个数而做相应的增长。出队列操作将数据从队列中移除，数据位于out offset。当移除完成的时候，out offset会根据移除数据的数量而坐相应的增长。当out offset和in offset相等的时候，表明队列是空的:这时候出队列操作是不允许的，直到有新的数据入队列。当in offset的长度等于队列的长度的时候，数据不允许入队列，直到队列被reset。

创建队列

为了使用kfifo，你必须先定义和初始化它。和大多数内核对象一样，你可以动态或者静态的创建。最通用的方法是动态的:

int kfifo_alloc(struct kfifo *fifo, unsigned int size, gfp_t gfp_mask);

这个方法创建一个大小为size字节kfifo队列。内核使用gfp_mask标志位来分配队列。成功后，kfifo_alloc()返回0; 如果出错则返回一个负数的错误码。下面是一个简单的例子:

struct kfifo fifo;
int ret;
ret = kfifo_alloc(&kifo, PAGE_SIZE, GFP_KERNEL);
if (ret)
    return ret;
/* ‘fifo’ now represents a PAGE_SIZE-sized queue ... */

如果你想自己分配buffer，你可以额使用下面的方法:

void kfifo_init(struct kfifo *fifo, void *buffer, unsigned int size);

这个方法使用大小为size的buffer来创建和初始化kfifo。无论是kfifo_alloc()还是kfifo_init()，size都必须是2的次幂。

静态的申明一个kfifo更简单，但是不通用:

DECLARE_KFIFO(name, size);
INIT_KFIFO(name);

入队列

当kfifo队列创建并且初始化好后，可以通过kfifo_in()方法来将数据入队列:

unsigned int kfifo_in(struct kfifo *fifo, const void *from, unsigned int len);

这个方法将从from开始的len个字节拷贝到队列中。如果成功，则返回入队列的字节数。如果队列可用空间少于len字节，那么函数只拷贝可用空间大小对应的字节数。因此，返回值可以小于len甚至为0，当没有任何数据拷贝的时候。

出队列

当通过kfifo_in()将数据入队列后，你可以通过kfifo_out()将数据从队列中移除。

unsigned int kfifo_out(struct kfifo *fifo, void *to, unsigned int len);

这个方法最多从队列拷贝len个字节的数据到to指向的buffer中。如果成功，则返回拷贝的字节数。如果队列中的数据少于len字节，那么拷贝的数据也将少于len。

当出队列操作完成，队列也就无法方法该数据了。这是队列的通常使用方法，但是如果你想从队列中peek数据，但是又不想移除它，那么你可以使用kfifo_out_peek():

unsigned int kfifo_out_peek(struct kfifo *fifo, void *to, unsigned int len,
unsigned offset);

这个方法和kfifo_out()类似，除了out offset不会增长。因此出队列的数据仍然可以通过kfifo_out()获取。参数offset用于指定队列的索引；0表示从头开始读取，此时和kfifo_out一致。

获取队列的大小

获取kfifo队列的buffer的大小，可以通过调用kfifo_size()来实现:

static inline unsigned int kfifo_size(struct kfifo *fifo);

kfifo_len() 用于获取kfifo中存储的数据长度:

static inline unsigned int kfifo_len(struct kfifo *fifo);

kfifo_avail() 用于获取kfifo的可用空间大小:

static inline unsigned int kfifo_avail(struct kfifo *fifo);

最后，kfifo_is_empty()和kfifo_is_full()返回非0如果给定的kfifo为空或者已满，如果不是则返回0:

static inline int kfifo_is_empty(struct kfifo *fifo);
static inline int kfifo_is_full(struct kfifo *fifo);

重置和销毁队列

可以通过kfifo_reset()重置kfifo，抛弃队列中的所有内容:

static inline void kfifo_reset(struct kfifo *fifo);

可以通过kfifo_free()销毁队列:

void kfifo_free(struct kfifo *fifo);

如果你通过kfifo_init()来创建队列，那么你有责任来释放对应的buffer。你需要根据你创建的情况来决定如何释放它。

队列的使用例子

在我们讨论了队列的接口之后，让我们来看一个kfifo的简单例子。加上我们创建一个大小为8KB的kfifo。我们可以将数据写入到队列中。在这个例子中，我们会将整数写入到队列。在你自己的代码中，你可能会将更复杂的数据结构写入到队列中。好了，让我们来看一下这个例子:

unsigned int i;
/* enqueue [0, 32) to the kfifo named ‘fifo’ */
for (i = 0; i < 32; i++)
    kfifo_in(fifo, &i; sizeof(i));

这个kfifo队列的名字叫做fifo，包含0到31。我们可以从队列中获取第一个元素然后验证它是否是0:

unsigned int val;
int ret;
ret = kfifo_out_peek(fifo, &val, sizeof(val), 0);
if (ret != sizeof(val))
    return -EINVAL;
printk(KERN_INFO “%u\n”, val); /* should print 0 */

为了将所有的数据出栈，我们可以使用kfifo_out():

/* while there is data in the queue ... */
while (kfifo_avail(fifo)) {
    unsigned int val;
    int ret;
    /* ... read it, one integer at a time */
    ret = kfifo_out(fifo, &val, sizeof(val));
    if (ret != sizeof(val))
        return -EINVAL;
    printk(KERN_INFO “%u\n”, val);
}

Maps

map ，是一个联合数组，是多个唯一key的合集，每个key和一个特定的value相关联。key和value之间的关系叫做mapping。Maps至少支持三个操作:

• Add(key, value)
• Remove(key)
• value = Lookup(key)

尽管hash table是一种map，但是不是所有的map都是通过hash实现的。除了使用hash table来实现map，map也可以使用自平衡二叉搜索树来存储数据。尽管hash提供了更好的复杂度，但是二叉搜索树在最坏的情况下有更好的表现。一个二叉搜索树提供了顺序存储的功能，因此用户可以将数据按序存储。最后，一个二叉搜索树不需要hash函数。

linux内核提供了一个简单但是高效的map数据结构，但是它不是一个通用的map。相反，它适用于某个特定的场景:将一个唯一的数字映射成一个指针。

二叉树

tree 结构提供了一个类似树的数据结构。数学上，这是一个非循环的，联通的，有向图。图中的每个节点有0个或者更多的出边，0个或者1个入边。二叉树最多有两个出边–也就是说一个节点有0个，1个或者2个子节点。

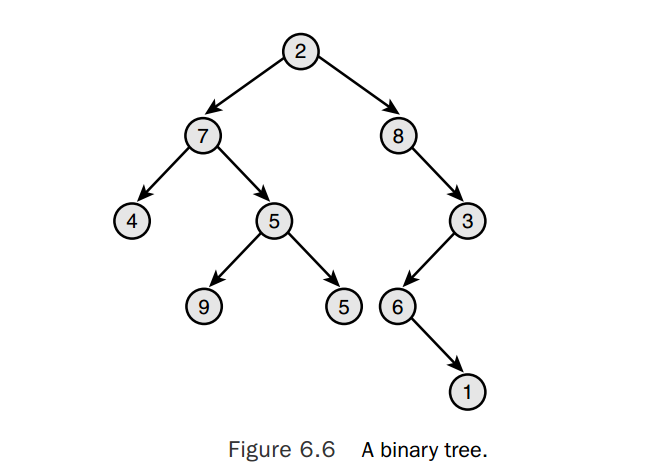
二叉搜索树

一个二叉搜索树是一个有序的二叉树。顺序按照下面的方式定义的:

• 根节点的值大于左子树所有节点的值
• 根节点的值小于右子树所有节点的值
• 所有的子树都是二叉搜索树

一个二叉搜索树是一个二叉树，所有的节点按照对应的顺序排序:左子节点小于父节点，右子节点大于父节点。因此，在二叉搜索树中搜索某个节点是高效的。

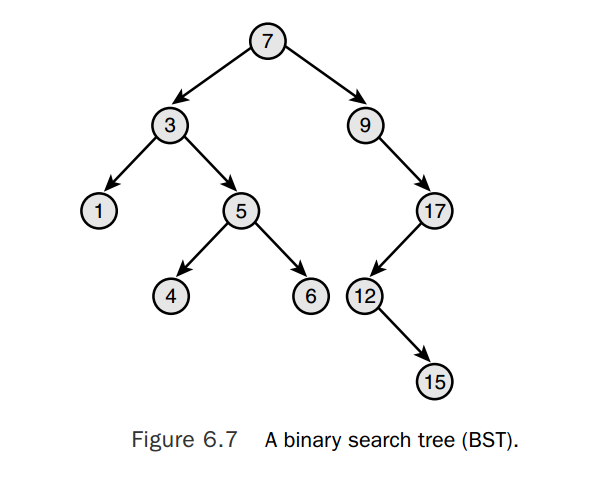
自平衡的二叉搜索树

一个节点的深度是按照该节点到根节点的父节点的数量。树底部的节点–没有子节点的节点–被称作叶子。树的深度是所有叶子结点深度的最大值。一个自平衡的二叉搜索树中，所有叶子结点的深度之间差距最大为1.一个自平衡的二叉搜索树是一个试图保持平衡的二叉树。

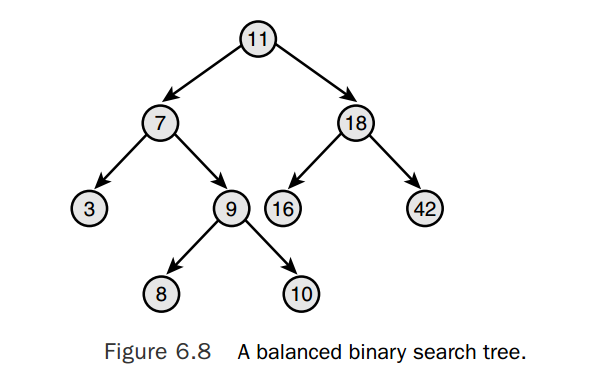
红黑树

红黑树是自平衡二叉树的一种。linux的主要二叉树是红黑树。红黑树的节点有一个特殊的颜色属性，该属性可能为红色也可能是黑色。红黑树会满足下面的六个条件，从而保持树的自平衡:

• 所有节点要么是红要么是黑
• 叶子结点是黑的
• 叶子结点不包含数据
• 所有非叶子结点有两个子节点
• 如果结点是红色的，那么它的子节点都是黑的
• 从一个结点到其每个叶子结点的所有路径包含相同数目的黑色结点。

当上面所有的条件都满足的时候，能够保证最深的叶子结点的高度不会超过最浅叶子结点的2倍。因此，树总是自平衡的。为什么会这样其实很简单。首先，根据条件5，一个红色的结点不会是另一个红色结点的子节点或者父节点。根据条件6，树的所有路径包含相同的黑色节点数。树的最长路径总是交替出现红色结点和黑色结点。树的最短路径，有相同的黑节点数，只包含黑色结点。因此从叶子结点到根节点的最长路径不会是从叶子结点到根节点的最短路径的两倍。

如果插入和删除操作都强制满足上面的六个条件，那么这棵树可以一直保持自平衡。现在，看起来似乎需要插入和删除满足上面的条件。Why not implement the operations such that they enforce other, simpler rules that result in a balanced tree? (这句话怎么翻译，不是很清楚)。事实证明这些条件相对容易满足，使得删除和添加在保持平衡树的前提下不会带来过多额外的消耗。

描述插入和删除是如何保持这些条件已经超出了本书的范围。尽管这些规则很简单，但是实现却很复杂。

rbtrees

linux实现的红黑树叫做rbtrees。定义在lib/rbtree.c中，声明在<linux/rbtree.h>中。除了优化之外，linux的红黑树和上面提到的红黑树类似。红黑树保持平衡，插入操作的复杂度通常是O(logn)的。

红黑树的根节点的结构是rb_root。为了创建新的树，我们需要分配一个新的rb_root，然后初始化成特殊的值RB_ROOT。

struct rb_root root = RB_ROOT;

红黑树中的节点的结构是rb_node。给定一个rb_node，我们可以向左访问也可以向右访问。

红黑树的实现没有提供搜索和插入功能。使用红黑树的用户需要自己定义这些方法。这是因为C语言不容易实现泛型编程，linux内核的开发者相信最高效实现搜索和插入的方法是每个用户在内核提供的红黑树帮助函数的基础上实现自己的比较运算符来实现搜索和插入功能。

最好的讲解查询和插入功能的方法是举一个现实中的例子。首先让我们来看一个搜索的例子。下面的函数实现了Linux文件页缓存的搜索。每个inode有自己的红黑树，红黑树存放的节点里的内容是内容在文件中的偏移。因此这个函数用来在红黑树中搜索某个偏移量:

struct page * rb_search_page_cache(struct inode *inode,
unsigned long offset)
{
    struct rb_node *n = inode->i_rb_page_cache.rb_node;
    while (n) {
        struct page *page = rb_entry(n, struct page, rb_page_cache)
        if (offset < page->offset)
            n = n->rb_left;
        else if (offset > page->offset)
            n = n->rb_right;
        else
            return page;
    }
    return NULL;
}

在这个例子中，while循环遍历红黑树，根据offset决定是向左子树搜寻还是向右子树搜寻。if和else表达式实现了红黑树的比较操作。如果循环找到了匹配的offset, 那么搜索就结束了，该方法返回了对应的 page 结构。如果循环遍历到红黑树的结尾都没有找到匹配的数据，则返回NULL。

插入相对来说更复杂一些，因为它不仅要实现搜索还需要实现插入逻辑。下面代码不是一个普通的方法，但是如果你需要实现自己的插入方法，那么这会是一个很好的指导:

struct page * rb_insert_page_cache(struct inode *inode,
                                   unsigned long offset,
                                   struct rb_node *node)
{
    struct rb_node **p = &inode->i_rb_page_cache.rb_node;
    struct rb_node *parent = NULL;
    struct page *page;
    while (*p) {
        parent = *p;
        page = rb_entry(parent, struct page, rb_page_cache);
        if (offset < page->offset)
            p = &(*p)->rb_left;
        else if (offset > page->offset)
            p = &(*p)->rb_right;
        else
            return page;
    }
    rb_link_node(node, parent, p);
    rb_insert_color(node, &inode->i_rb_page_cache);
    return NULL;
}

和搜索类似，上面的代码也会遍历红黑树。和搜索不同的是，这个方法不是找到匹配的offset，而是为新的offset找到一个新的插入点。当插入点找到的时候，调用rb_link_node()来插入新的节点。然后调用rb_insert_color() 来完成复杂的平衡操作。如果page cache成功的添加到红黑树中，则返回NULL。

什么时候采用什么数据结构

算法复杂度